青年教师高效课堂大赛优秀案例（七）

                                                                 廉洪英

《两角和与差的余弦》教学设计

一、教材分析

本节课是新课标人教B版必修三第八章第二单元第一节的内容，本节是在三角函数以及向量的数量积的基础上进行学习的，为后面学习两角和与差的正弦、正切奠定基础，本节课起着承前启后的作用，在高考中也是重点考查内容之一，同时也是培养学生数学能力的良好题材，两角和与差的余弦是从学生探究特殊角差的余弦值开始，通过具体角抽象出任意角的差的余弦模型，无论在知识上，还是方法上对学生今后的学习都有积极的意义。

二、学情分析

对于我校的高中学生，知识经验比较贫乏，虽然他们的智力发展已到了形式运演阶段，但并不具备较强的抽象思维能力和演绎推理能力，所以我在授课时从具体的特殊角出发，注重引导、启发、研究和探讨以符合这类学生的心理发展特点，从而促进思维能力的进一步发展。本节课我采用启发式、讨论式以及讲练结合的教学方法，通过问题激发学生求知欲，使学生主动参与数学实践活动，以独立思考和相互交流的形式，在教师的指导下发现、分析和解决问题。

三、教学目标

1． 知识与技能

（1）能利用三角函数的定义与向量知识推导出两角差的余弦公式，进一步体会向量的作用.（2）掌握两角和与差的余弦公式，理解公式的结构，能够运用公式解决相关问题.

（3）体会公式运用中一般与特殊的转化关系.

2．过程与方法

在公式的推导、应用过程中，培养学生的观察、分析、归纳能力和严密的逻辑思维的能力，体验从特殊到一般，一般到特殊的认知规律，提高熟悉猜想和归纳的能力。 

3．情感、态度与价值观

通过教师指导下学生的自主学习、相互交流和探索活动，培养学生主动探索、用于发现的求知精神，激发学生的学习兴趣，让学生感受到成功的喜悦。在解决问题的过程中，使学生养成细心观察、认真分析、善于总结的良好习惯。

四、教学重点与难点

教学重点：①两角和与差公式的推导；②两角和与差公式的正用、逆用

教学难点：①理解公式的结构及公式中的角可以是几个角的和与差；②两角和与差公式的推导过程．

五、教法与学法

1．教法

①启发引导法：这种方法有利于学生对知识进行主动建构；有利于突出重点，突破难点；有利于调动学生的主动性和积极性，发挥其创造性．

②分组讨论法：有利于学生进行交流，及时发现问题，解决问题，调动学生的积极性．

③讲练结合法：可以及时巩固所学内容，抓住重点，突破难点．

2．学法

引导学生首先从15°的余弦值求法出发，发现直接拆解公式有误，进而探究正确的求法，继续猜想换为任意角后仍成立，采用类比的方法进行证明，最终得到两角差的余弦，进而采用换元的方法得到两角和的余弦公式，概括公式结构，可以对各种能力的同学引导推导的思维方法。

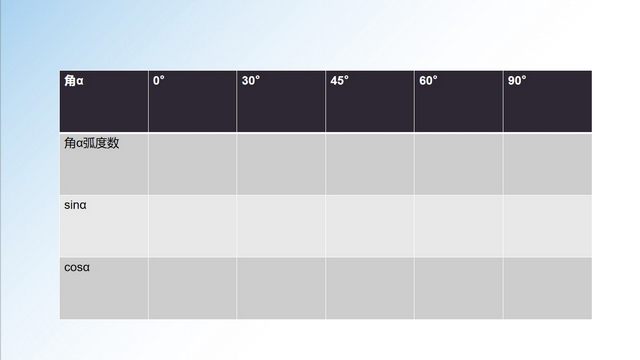
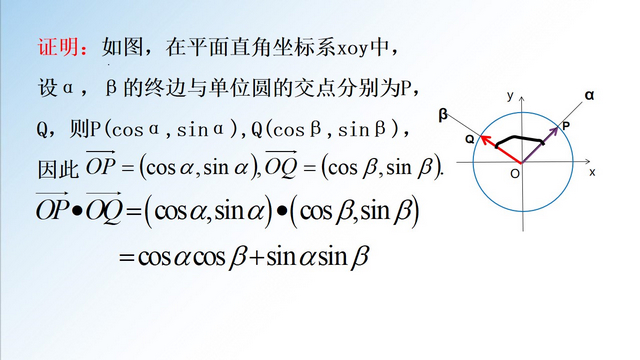
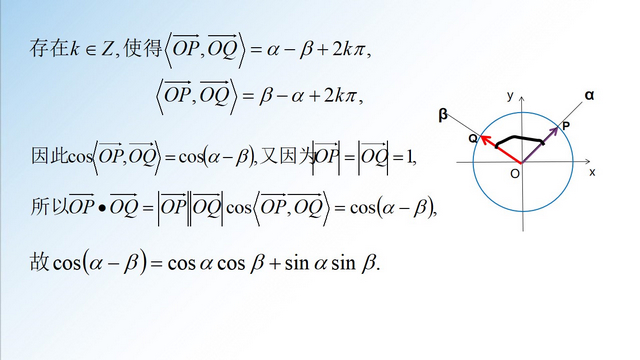
                                                               课后感悟   

     学起于思，思源于疑，教学实质上就是设疑、质疑、解疑的过程，本节课我在课堂上给学生提出问题，有了疑问，学生就会积极思考，我在其中承担着授业、解惑的责任。先让学生找到错误点，然后去探究正确的算法，进而用类比的方法将特殊推广到一般。通过有层次的设置问题，引导学生参与到课堂中来，激励学生去寻找“柳暗花明又村”的感觉，当学生得到成功喜悦的同时，他们的创造思维能力也得到了发展。解决好这些问题可以培养学生的创造思维能力，理解能力，分析问题和解決问题能力。

    课堂教学是一门遗憾的艺术，课后我回顾并进行诊断，开出了自己的“病历”，第一，自己整堂课话语较多，第二学生讲解较少。针对这些问题，在今后的教学中我会加以改进，让自己的课堂充盈起来。